časovna vrednost denarja

Logiranje

Logirate se tako, da kliknete na LOGIN
Odpre se slika na desni.
Vpišete email in password in kliknete Sign in
Če ne želite biti več logirani se izpišete tako, da kliknete LOGOUT

V kolikor še nimate uporabniškega imena in gesla se morate najprej registrirati.
Kliknete Sign up now in dobite sliko spodaj levo.

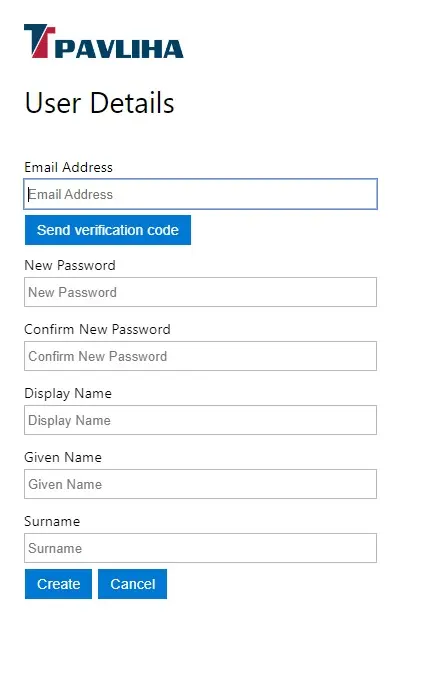
Registracija

Vpišete email, ki ga boste uporabljali pri prijavi.
Kliknete Send verification code. Na vaš email bo poslana verifikacijska koda
Preverite email. Če morda ne najdete emaila, preverite če je v spamu

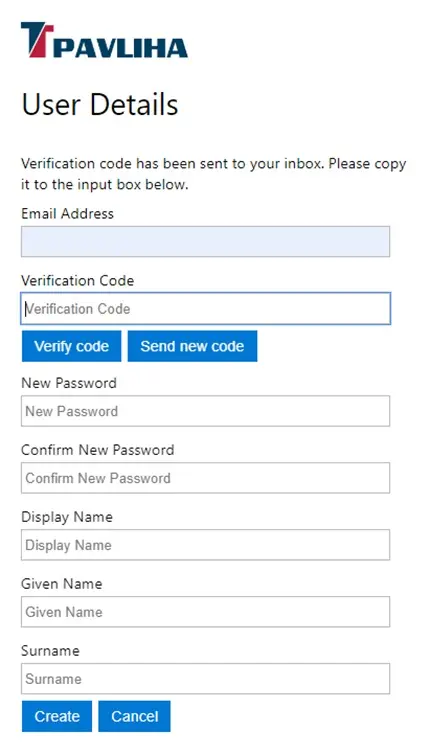
Pomoč pri registriranju - vpiši verification code

Verifikacija

Vpišite verifikacijsko kodo. Če morda ne velja več, ker je preteklo preveč časa, kliknite Send new code in poslana vam bo nova koda.
Kliknite Verify code
Določite še geslo. To naj bo sestavljeno iz malih in velikih črt, znakov in številk. Dolžina gesla naj bo vsaj 8 znakov.
V vrtico Confirm New Password geslo vpišite še enkrat, da ne bi bilo napake.
Display Name bo vaše prikazno ime in je poljubno.
Given name je osebno ime.
Surname je priimek.
Na koncu kliknete na Create in vrnili se boste na začetno stran.

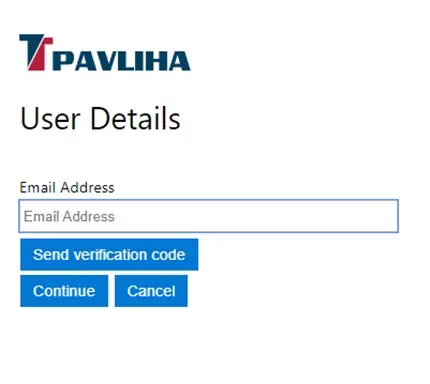
Pomoč pri pozabljenem geslu - vpiši email

Pozabljeno geslo

Če ste pozabili geslo kliknite Forgot your passwod? na prvi sliki.
Vpišite svoj email in kliknite Send verification code.
Preveri svoj email in nadaljujte na naslednji sliki oz. kliknite gumb Continue

Pomoč pri pozabljenem geslu - vpiše verification code

Pozabljeno geslo - verifikacija

Vpišite verifikacijsko kodo, ki ste jo dobili v emailu.
Kliknite Verify code oz. kliknite Send new code v kolikor potrebujete novo kodo zaradi preteka časa.
Potem kliknite Continue in nadaljujte na naslednji sliki.

Pomoč pri pozabljenem geslu - vpiši nov password

Pozabljeno geslo - novo geslo

Vpišite novo geslo in ga zaradi morebitne napake pri vnosu vnesite ponovno v polje Confirm New Password
Na koncu Continue
In geslo je spremenjeno oz. bo veljalo novo geslo.

Določite skupino bloga

Zaprete oz. odprete celoten iskalnik. Iskalnik je v obliki drevesa.
Prikažejo se samo skupine drevesa.
Prikažejo se skupine in podskupine drevesa
Prikažejo se tretji nivo drevesa.
Prikažejo se postavke zadnjega, četrteka nivoja drevesa
Iskalnik se resetira

S klikom na posamezno poglavje odpirate in zapirate veje drevesa. Če kliknete vejo drevesa pod katero ni druge veje drevesa, sprožite iskanje.

DEJAVNOST
RAČUNALNIŠTVO
EKONOMIJA
PRAVO
PSIHOLOGIJA
ZGODOVINA
POLITIKA

ČASOVNA VREDNOST DENARJA

Časovna vrednost denarja je povezana s konceptoma inflacije in kupne moči. Upoštevati je treba oba dejavnika skupaj s stopnjo donosa, ki jo lahko dobimo z vlaganjem denarja.

ČASOVNA VREDNOST DENARJA

Ekonomski subjekt zahteva določeno nadomestilo zato, da se danes odreče uporabi razpoložljivega denarja. In čim daljši je čas, za katerega se odreče uporabi denarja, večje je nadomestilo. To nadomestilo pa imenujemo donos.

Torej ima enaka denarna enota za ekonomske subjekte različno vrednost glede na to, kdaj v času se porabi. Cilj poslovanja podjetja je maksimiziranje tržne vrednosti, ki je tem večja, če lastnikom prinese več denarja. Ni pa pomembna samo količina denarja, ampak tudi časovna razporeditev denarja.

PRIHODNJA VREDNOST

SPLOŠNO

Prihodnja vrednost označuje vsoto denarja, na katero bo narasla naložba v določenem časovnem obdobju. Če je to časovno obdobje daljše od časovnega obdobja, za katerega se obračunavajo obresti, se pri izračunu uporablja obrestno obrestni račun.

ENO PLAČILO

Če želimo izračunati, koliko bo vredna vloga v banki v enem letu, če se obresti pripišejo po enem letu, uporabimo formulo :

FV = PV ( 1 + R )

FV - future value oz. prihodnja vrednost
PV - glavnica
r - obrestna mera

Banka običajno pripisuje obresti ob koncu leta, oz. ob koncu določenega obdobja, ki je lahko tudi pol leta. Torej, če imamo glavnico npr. 1000€ in obrestno mero 10%, bo prihodnja vrednost ob koncu leta 1100€. V drugem letu se obrestuje znesek 1100€ in prihodnja vrednost ob koncu drugega leta je 1.210€. Formula za ta izračun pa je naslednja :

FV = {PV ( 1 + r )}^{n}

FV - prihodnja vrednost
r - obrestna mera
n - število obdobij obrestovanja
(1+r)n - faktor prihodnje vrednosti

PRIMER 1

Glavnica = 1,000€
Letna obrestna mera = 10%
Število obdobij = 2

FV = {1000 ( 1 + 0,10 )}^{2} = 1210

PRIMER 2

Koliko bo vredna začetna naložba 100€ čez sedem let pri letni obrestni meri 9%.

FV = {1000 ( 1 + 0,09 )}^{7} = 182,80

PRIMER 6

Na razpolago imamo 100 000€, ki jih lahko investiramo za 3 leta. Obrestne mere na hranilne vloge znašajo 5%, medtem ko državne obveznice prinašajo 8% letne obresti. Koliko bo vrednih naših 100 000€ čez tri leta, če jih vložimo na hranilno knjižico ali če kupimo državne obveznice.

{FV}_{vloga} = {100.000 x  1,05}^{3} = 115.762,50 €

{FV}_{obveznice} = {100.000 x  1,08}^{3} = 125.971,20 €

PRIMER 7

Študent Peter želi na smučanje, to pa ga bo stalo 3.000€. Leta 1990 znašajo njegovi prihranki 2.253,94€. Po najmanj kakšni obresti meri mora Peter naložiti svoje prihranke leta 1990, da bo imel čez tri leta dovolj denarja za smučanje?

Izpeljemo obrazec:

r = \sqrt[n]{\frac{FV}{PV}} - 1

in vstavimo podatke:

r = \sqrt[3]{\frac{3000}{2253,94}} - 1

Peter bi moral naložiti svoje prihranke vsaj po 10% letni obrestni meri.

PRIMER 8

Kolikšna je stopnja donosa investicije, pri kateri morate danes plačati polog 40.000€ in dobite čez 10 let izplačanih 100.000€?

Izpeljemo enačbo:

r = \sqrt[n]{\frac{FV}{PV}} - 1

in vstavimo podatke:

r = \sqrt[n]{\frac{100.000}{40.000}} - 1

Stopnja donosa je 9,59%.

PRIMER 9

Poslovni partner nam ponuja naložbo, ki obljublja izplačilo 60.000€ ob koncu šestega leta in 60.000€ ob koncu dvanajstega leta. Zahtevana donosnost je 10%. Koliko moramo vložiti danes, da bomo dobili ta izplačila?

Enačba za sedanjo vrednost večkratnih plačil je:

PV = \sum_{t = 1}^{n} R_{t} x {(\frac{1}{1 + r})}^{t}

Vstavimo naše podatke in dobimo:

60.000€ x {(\frac{1}{1,1})}^{6} + 60.000€ x {(\frac{1}{1,1})}^{12} = 52.986,27€

PRIMER 10

Pred kratkim smo zadeli na loteriji. Zadetek je izplačljiv na dva načina:

enkratno izplačilo v višini 1.125.000€
plačilo 350.000€ danes in še 60.000€ vsako leto prihodnjih 20 let.
Diskontna stopnja je 8%

Iz izračuna v Excelovi tabeli je vidno, da je današnja vrednost prihodnjih donosov 971.297,24€. Glede na to, da je takojšnje izplačilo 1.125.000€ se bomo odločili za takojšnje izplačilo.

PRIMER 13

Franc Koren ima na razpolago € 100.000, ki jih je pripravljen investirati za obdobje treh let. Obrestne mere na hranilne vloge trenutno znašajo 6 %, medtem ko državne obveznice prinašajo 8 %-ne letne obresti. Izračunajte, koliko bo vrednih Francetovih € 100.000 čez tri leta, če jih vloži na hranilno knjižico ali če kupi državno obveznico!

Uporabimo enačbo

FV = {PV ( 1 + r )}^{n}

in izračunamo

{100.000 x 1,08}^{3} = 125.971, 20€

{100.000 x 1,06}^{3} = 119.101, 60€

PRIMER 14

V začetku leta t-1 ste na hranilno knjižico vložili € 60.000. Čez eno leto ste vložili dodatnih € 80.000 in čez dve leti še € 100.000. Konec leta t+3 želite dvigniti s hranilne knjižice vse prihranke, ki so se obrestovali po 8 %-ni letni obrestni meri. Koliko denarja boste dvignili?

t-1	t	t+1	t+2	t+3
60.000	80.000		100.000	dvig

{60.000 x 1,08}^{4} = 81.629,33€

{80.000 x 1,08}^{3} = 100.776,96€

{100.000 x 1,08}^{1} = 108.000€

Skupaj bo dvig znašal 290.406,29€.

PRIMER 15

Študent VŠP Sebastian se zelo rad smuča in želi zimo leta t+3 preživeti v Vailu v ZDA. Meni, da bi ga to stalo približno € 2.100. Danes, leta t, znašajo njegovi prihranki natanko € 1.500. Po najmanj kakšni obrestni meri mora Sebastian naložiti svoje prihranke danes, leta t, da bo imel čez tri leta dovolj denarja za smučanje v ZDA?

Iz enačbe

FV = {PV ( 1 + r )}^{n}

preračunamo enačbo

r = \sqrt[n]{\frac{FV}{PV}} - 1

in dobimo rezultat

r = \sqrt[3]{\frac{2100}{1500}} - 1 = 11,87%

VEČKRATNA PLAČILA

V praksi pa se v glavnem dogaja, da imamo več različnih vplačil v različnih časovnih obdobjih. V takem primeru pa moramo za vsako vplačilo posebej izračunati, kakšna bo prihodnja vrednost. Splošna enačba prihodnje vrednosti za večkratna vplačila je naslednja :

{FV}_{n} = \sum_{t = 0}^{+ n-1} I_{t} x {FVIF}_{(n-1)}

Pri čemer je FVIF = (1+r)n , torej faktor prihodnje vrednosti
n - število obdobij obrestovanja
It - glavnica obdobja t

PRIMER 3

V začetku prvega leta vložimo na banko 1000€, v začetku drugega 500€ in v začetku tretjega leta 600€. Kolikšna je prihodnja vrednost na koncu tretjega leta, če je letna obrestna mera 9%?

Enačba

{FV}_{n} = \sum_{t = 0}^{+ n-1} I_{t} x {FVIF}_{(n-1)}

v tem primeru zgleda takole

{FV}_{3} = I_{0} {(1+r)}^{3} + I_{1} {(1+r)}^{2} + I_{2} {(1+r)}^{1}

PRIMER 11

Zavarovalniški zastopnik bi vas rad navdušil za naslednjo obliko zavarovanja. V primeru, da prihodnjih 10 let vsako leto plačate zavarovalnici 150.000€ boste od 25. leta dalje dobivali 15 let vsako leto 250.000€. Diskontna stopnja je 6%. Ali bi se odločili za to zavarovanje?

Leto n	Vložen znesek	Diskontni faktor	Današnja vrednost vplačanega zneska		Leto n	Izplačan znesek	Diskontni faktor	Današnja vrednost izplačanega zneska
1	150.000,00 €	0,9434	141.509,43 €	1	25	250.000,00 €	0,2330	58.249,66 €
2	150.000,00 €	0,8900	133.499,47 €	2	26	250.000,00 €	0,2198	54.952,51 €
3	150.000,00 €	0,8396	125.942,89 €	3	27	250.000,00 €	0,2074	51.841,99 €
4	150.000,00 €	0,7921	118.814,05 €	4	28	250.000,00 €	0,1956	48.907,54 €
5	150.000,00 €	0,7473	112.088,73 €	5	29	250.000,00 €	0,1846	46.139,18 €
6	150.000,00 €	0,7050	105.744,08 €	6	30	250.000,00 €	0,1741	43.527,53 €
7	150.000,00 €	0,6651	99.758,57 €	7	31	250.000,00 €	0,1643	41.063,71 €
8	150.000,00 €	0,6274	94.111,86 €	8	32	250.000,00 €	0,1550	38.739,35 €
9	150.000,00 €	0,5919	88.784,77 €	9	33	250.000,00 €	0,1462	36.546,56 €
10	150.000,00 €	0,5584	83.759,22 €	10	34	250.000,00 €	0,1379	34.477,88 €
			1.104.013,06 €	11	35	250.000,00 €	0,1301	32.526,30 €
				12	36	250.000,00 €	0,1227	30.685,19 €
				13	37	250.000,00 €	0,1158	28.948,30 €
				14	38	250.000,00 €	0,1092	27.309,71 €
				15	39	250.000,00 €	0,1031	25.763,88 €
								599.679,29 €

Iz primerjave neto sedanje vrednosti vplačil in izplačil sledi, da je neto sedanja vrednost vplačil 1.104.013,06€, neto sedanja vrednost izplačil pa 599.679,29€. Torej se za to naložbo ne bomo odločili.

SEDANJA VREDNOST

SPLOŠNO

Sedanja vrednost je ravno nasprotni pojem od prihodnje vrednosti. Gre za to, da izračunamo, koliko je nek prihodnji donos vreden danes. Če imamo npr. možnost vlagati prihranke v nekaj različnih naložb, za katere vemo, da nam bo prva npr. prinesla drugo leto 130€, druga čez leto in pol 150€, nas zanima, koliko pa sta ta dva donosa vredna danes.

ENO PLAČILO

Enačba za eno plačilo je naslednja :

PV = \frac{{FV}_{n}}{{(1+r)}^{n}}

PV - sedanja vrednost
FV - Prihodnja vrednost
r - diskontna stopnja
n - število obdobij

PRIMER 4

Koliko moramo vložiti v banko danes, da bomo čez 4 leta lahko kupili avto za 20.000€, če je letna obrestna mera 6%?

PV = \frac{20.000€}{{(1 + 0,06 )}^{4}} = \frac{20.000€}{1,2624} = 15.842,84

VEČKRATNA PLAČILA

Če pa imamo opravka z več plačili, ki jih bomo dobili v prihodnosti, pa uporabimo naslednjo enačbo:

PV = \sum_{t = 1}^{n} R_{t} x {(\frac{1}{1 + r})}^{t}

R - plačila
r - diskontna stopnja
n - število obdobij

PRIMER 5

Državna obveznica nam obljublja naslednja izplačila vsak konec leta in sicer konec prvega leta 1.000€, konec drugega 1.100€, konec tretjega leta pa 1.200€. Diskontna stopnja je 8%. Izračuna neto sedanjo vrednost.

Enačba:

PV = \sum_{t = 1}^{n} R_{t} x {(\frac{1}{1 + r})}^{t}

za posebni primer zgleda takole:

PV = R_{1} x {(\frac{1}{1 + r})}^{1} + R_{2} x {(\frac{1}{1 + r})}^{2} + R_{3} x {(\frac{1}{1 + r})}^{3}

Donosi	DF	R x DF
1.000,00€	0,9259	925,90€
1.100,00€	0,8573	943,03€
1.200,00€	0,7938	952,56€
3.300,00€		2.821,49€

Donosi državnih obveznic so na današnji dan vredni 2.821, 49€.

PRIMER 12

Kolikšna je stopnja donosnosti investicije, pri kateri morate danes plačati polog € 400.000 in dobite čez 10 let izplačanih € 1 mio?

Poslovni partner pa vam ponuja naložbo, ki obljublja izplačilo € 600.000 ob koncu šestega leta ter € 600.000 ob koncu dvanajstega leta. Glede na tveganje je zahtevana stopnja donosa 10 %.

Kateri investiciji bi dali prednost, če bi se morali odločiti le za eno izmed obeh možnosti?

Iz enačbe:

FV = {PV(1+r)}^{n}

izračunamo

r = \sqrt[10]{\frac{1.000.000}{400.000}} - 1 = 9,6%

Stopnja donosnosti investicije je 9,6%.

Za izračun neto sedanje vrednosti prihodnjih donosov uporabimo enačbo:

PV = \frac{{FV}_{n}}{{(1+r)}^{n}}

in sicer je neto sedanja vrednost dveh plačil po 600.000€ na koncu šestega in dvanajstega leta:

PV = \frac{{600.000}_{}}{{1,1}^{6}} + \frac{{600.000}_{}}{{1,1}^{12}} = 529.876, 23€

Odločil bi se za drugo možnost, ker je neto sedanja vrednost 529.876,23€ in to je več kot 400.000€.

O meni
Oglasi
Nov oglas za delo
Išči oglase za delo
Davčni register
iana
Nov blog
Pregled blogov
Moje računovodstvo
Prosti čas

O meni
Oglasi
Nov oglas za delo
Išči oglase za delo
Davčni register
iana
Nov blog
Pregled blogov
Moje računovodstvo
Prosti čas

Registracija

Verifikacija

Pozabljeno geslo

Pozabljeno geslo - verifikacija

Pozabljeno geslo - novo geslo

Glavni menu