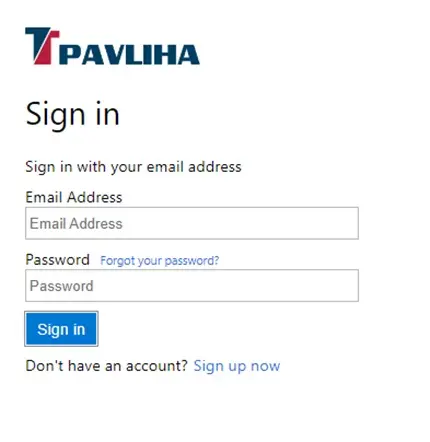
Logiranje
Logirate se tako, da kliknete na LOGIN
Odpre se slika na desni.
Vpišete email in password in kliknete Sign in
Če ne želite biti več logirani se izpišete tako, da kliknete LOGOUT
V kolikor še nimate uporabniškega imena in gesla se morate najprej registrirati.
Kliknete Sign up now in dobite sliko spodaj levo.
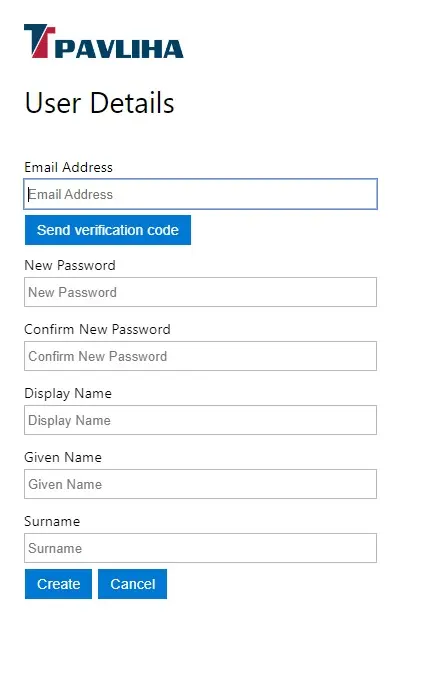
Registracija
Vpišete email, ki ga boste uporabljali pri prijavi.Kliknete Send verification code. Na vaš email bo poslana verifikacijska koda
Preverite email. Če morda ne najdete emaila, preverite če je v spamu
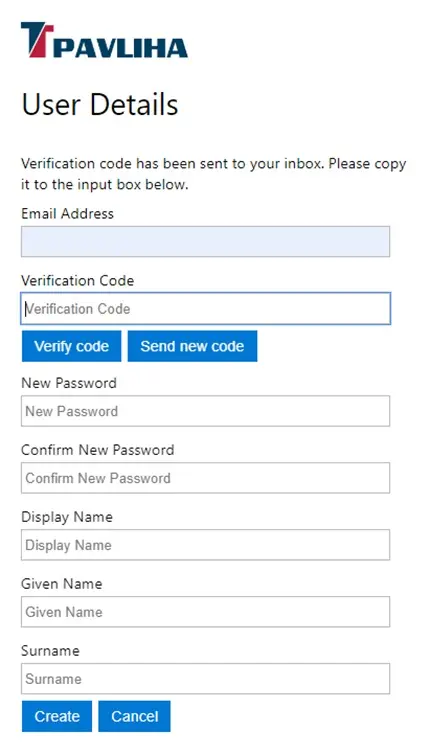
Verifikacija
Vpišite verifikacijsko kodo. Če morda ne velja več, ker je preteklo preveč časa, kliknite Send new code in poslana vam bo nova koda.Kliknite Verify code
Določite še geslo. To naj bo sestavljeno iz malih in velikih črt, znakov in številk. Dolžina gesla naj bo vsaj 8 znakov.
V vrtico Confirm New Password geslo vpišite še enkrat, da ne bi bilo napake.
Display Name bo vaše prikazno ime in je poljubno.
Given name je osebno ime.
Surname je priimek.
Na koncu kliknete na Create in vrnili se boste na začetno stran.
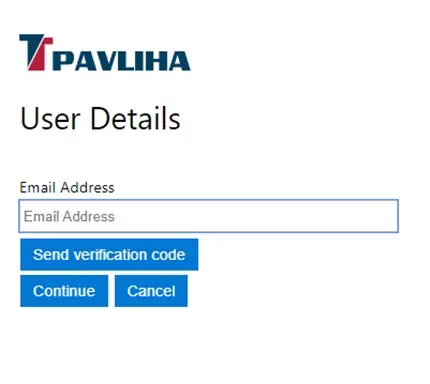
Pozabljeno geslo
Če ste pozabili geslo kliknite Forgot your passwod? na prvi sliki.Vpišite svoj email in kliknite Send verification code.
Preveri svoj email in nadaljujte na naslednji sliki oz. kliknite gumb Continue
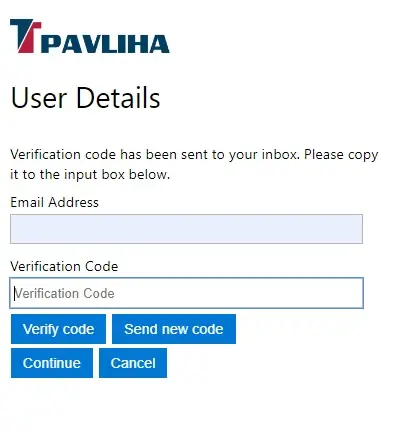
Pozabljeno geslo - verifikacija
Vpišite verifikacijsko kodo, ki ste jo dobili v emailu.Kliknite Verify code oz. kliknite Send new code v kolikor potrebujete novo kodo zaradi preteka časa.
Potem kliknite Continue in nadaljujte na naslednji sliki.
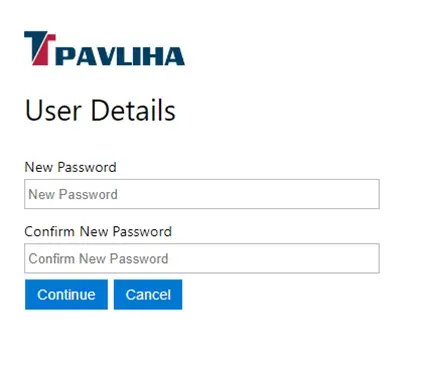
Pozabljeno geslo - novo geslo
Vpišite novo geslo in ga zaradi morebitne napake pri vnosu vnesite ponovno v polje Confirm New PasswordNa koncu Continue
In geslo je spremenjeno oz. bo veljalo novo geslo.

Glavni menu
- O meni
- Oglasi
- Nov oglas za delo
- Išči oglase za delo
- Davčni register
- iana
- Nov blog
- Pregled blogov
- Moje računovodstvo
- Prosti čas